I modsætning til er standardafvigelsen kvadratroden af den numeriske værdi opnået under beregning af varians. Mange mennesker kontrasterer disse to matematiske begreber. Så denne artikel gør et forsøg på at kaste lys på den vigtige forskel mellem varians og standardafvigelse.
Sammenligningstabel
| Grundlag for sammenligning | varians | Standardafvigelse |
|---|---|---|
| Betyder | Varians er en numerisk værdi, der beskriver variationen af observationer fra dets aritmetiske gennemsnit. | Standardafvigelse er et mål for spredning af observationer inden for et datasæt. |
| Hvad er det? | Det er gennemsnittet af kvadratiske afvigelser. | Det er root mean square afvigelsen. |
| Mærket som | Sigma-kvadreret (σ ^ 2) | Sigma (σ) |
| Udtrykt i | Kvadratiske enheder | Samme enheder som værdierne i datasættet. |
| indikerer | Hvor langt individer i en gruppe er spredt ud. | Hvor mange observationer af et datasæt adskiller sig fra dets gennemsnit. |
Definition af variant
I statistik defineres varians som måleen for variabilitet, der repræsenterer, hvor langt medlemmer af en gruppe er spredt ud. Det finder ud af den gennemsnitlige grad, som hver observation varierer fra den gennemsnitlige. Når variansen af et datasæt er lille, viser det datapunkternes nærhed til gennemsnittet, medens en større værdi af varians repræsenterer, at observationerne er meget spredt omkring det aritmetiske middel og fra hinanden.
For uklassificerede data :
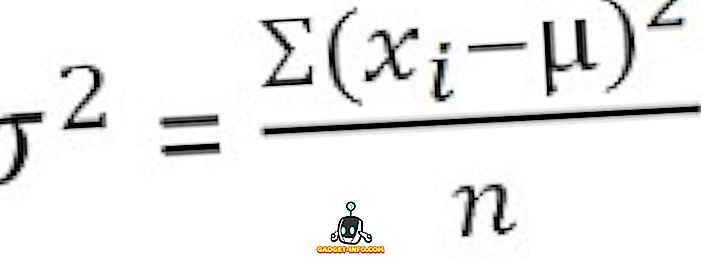
For grupperet frekvensfordeling :
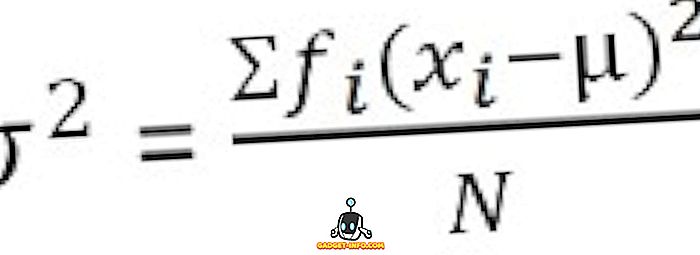
Definition af standardafvigelse
Standardafvigelse er et mål, der kvantificerer mængden af spredning af observationerne i et datasæt. Den lave standardafvigelse er en indikator for nærværet af scorerne til det aritmetiske gennemsnit og en høj standardafvigelse repræsenterer; scorerne spredes over et højere værdiforløb.
For uklassificerede data :

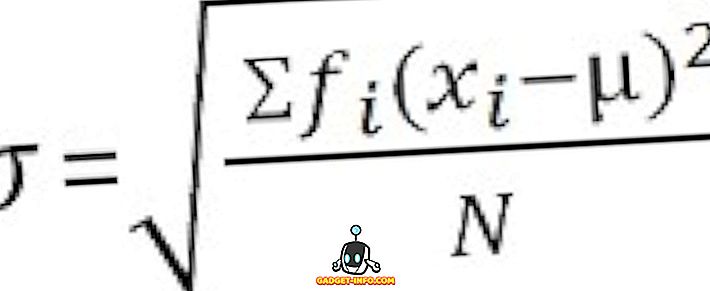
Nøgleforskelle mellem variation og standardafvigelse
Forskellen mellem standardafvigelse og varians kan trækkes tydeligt af følgende grunde:
- Varians er en numerisk værdi, der beskriver variationen af observationer fra dets aritmetiske gennemsnit. Standardafvigelse er et mål for spredning af observationer inden for et datasæt.
- Variansen er ikke andet end et gennemsnit af kvadratiske afvigelser. På den anden side er standardafvigelsen root mean square deviation.
- Variansen er betegnet med sigma-kvadreret (σ2), mens standardafvigelsen er mærket som sigma (σ).
- Variansen udtrykkes i kvadratiske enheder, som normalt er større end værdierne i det givne datasæt. I modsætning til standardafvigelse, som udtrykkes i de samme enheder som værdierne i datasættet.
- Variansen måler, hvor langt personer i en gruppe er spredt ud. Omvendt måler Standard Deviation hvor meget observationer af et datasæt adskiller sig fra dets gennemsnit.
Illustration
Punkter scoret af en studerende i fem fag er henholdsvis 60, 75, 46, 58 og 80. Du skal finde ud af standardafvigelsen og variansen.
Først og fremmest er du nødt til at finde ud af den gennemsnitlige,

Så de gennemsnitlige (gennemsnitlige) karakterer er 63, 8
Nu beregner variansen
| x | EN | (Xa) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14, 44 |
| 75 | 63.8 | 11.2 | 125, 44 |
| 46 | 63.8 | -17, 8 | 316, 84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262, 44 |
Hvor, X = Observationer
A = Aritmetisk middel
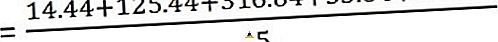
Og standardafvigelsen er -

ligheder
- Både varians og standardafvigelse er altid positive.
- Hvis alle observationer i et datasæt er identiske, vil standardafvigelsen og variansen være nul.
Konklusion
Disse to er grundlæggende statistiske termer, som spiller en afgørende rolle i forskellige sektorer. Standardafvigelse foretrækkes over gennemsnittet, da det udtrykkes i de samme enheder som målingerne, mens variansen udtrykkes i enhederne større end det givne datasæt.