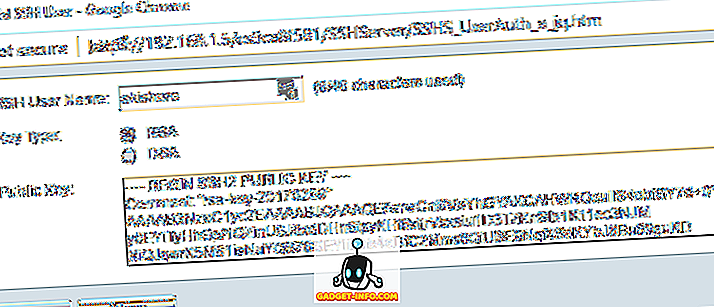
En anden forskel mellem B-træet og det binære træ er, at B-træet skal have alle dets barnnoter på samme niveau, mens binærtræ ikke har en sådan begrænsning. Et binærtræ kan have maksimalt 2 subtre eller knuder, mens i B-træ kan have M ingen af subtre eller knuder, hvor M er B-træets rækkefølge.
Sammenligningstabel
| Grundlag for sammenligning | B-tree | Binærtræ |
|---|---|---|
| Væsentlig begrænsning | En knude kan have ved max M antal børne noder (hvor M er træets rækkefølge). | En knude kan have på max 2 antal subtre. |
| Brugt | Den bruges, når data lagres på disken. | Det bruges, når optegnelser og data gemmes i RAM. |
| Træets højde | log M N (hvor m er rækkefølgen af M-vejetræet) | log 2 N |
| Ansøgning | Kode indeksering datastruktur i mange DBMS. | Kodeoptimering, Huffman-kodning osv. |
Definition af B-træ
Et B-træ er det afbalancerede M-vejetræ og også kendt som det balancerede sort træ. Det ligner binært søgetræ, hvor knudepunkterne er organiseret på basis af inorder-traversal. B-træets rumkompleksitet er O (n). Indsætnings- og sletningstidskompleksiteten er O (log n).
Der er visse betingelser, der skal være sandt for et B-træ:
- Træets højde skal ligge så lavt som muligt.
- Over træets blade bør der ikke være nogen tomme subtre.
- Træets blade skal komme på samme niveau.
- Alle knudepunkter skal have mindst antal børn undtagen forlade knudepunkter.
Egenskaber for B-træ i rækkefølge M
- Hver knude kan have maksimalt M antal børn og minimum M / 2 antal børn eller et hvilket som helst nummer fra 2 til maksimum.
- Hver knude har en nøgle mindre end børn med maksimale M-1 nøgler.
- Arrangementet af nøglerne er i en bestemt rækkefølge inden for noderne. Alle nøgler i undertræet til venstre for nøglen er forgængere af nøglen, og det til stede i højre side af nøglen hedder efterfølgere.
- På tidspunktet for indsætningen af en hel knude splittes træet i to dele, og nøglen med medianværdien indsættes ved moderknude.
- Fusionsoperationen finder sted, når knuderne slettes.
Definition af binærtræ
Et binært træ er en træstruktur, der højst kan have to pointer til sine barneknuder. Det betyder, at den højeste grad en knude kan have, er 2, og der kunne også være nul eller en-grader knudepunkt.
Der er visse varianter af et binært træ, såsom strengt binærtræ, komplet binærtræ, forlænget binærtræ osv.
- Det strengt binære træ er et træ, hvor hver ikke-terminal knude skal have forladt subtree og højre subtree.
- Et træ kaldes et komplet binærtræ, når det opfylder betingelsen om at have 2 jeg noder på hvert niveau, hvor jeg er niveauet.
- Gevindet binært er et binært træ, som består af enten 0 nej noder eller 2 antal noder.
Traversal Techniques
Træetransversal er en af de hyppigste operationer, der udføres på trædatastrukturen, hvor hver knude besøgte nøjagtigt en gang systematisk.
- Inorder-I dette træ traversal den venstre subtree er besøgt rekursivt derefter root node er besøgt og i sidste højre undertræ er besøgt.
- Preorer- I dette trækryds bliver rodnoden besøgt først og derefter venstre undertræ og til sidst højre undertræ.
- Postorder - Denne teknik besøger venstre undertræ, derefter højre undertræ og til sidst rodknude.
Nøgleforskelle mellem B-træ og binærtræ
- I B-træet kan det maksimale antal børnetoder, som en ikke-terminal knude har, være M, hvor M er B-træets rækkefølge. På den anden side kan et binærtræ højst have to subtre eller barnnoter.
- B-træ bruges når data lagres i disken, mens binær træ bruges, når data gemmes i hurtig hukommelse som RAM.
- Et andet anvendelsesområde for B-træ er kodeindeksering datastruktur i DBMS, i modsætning hertil, Binærtræ anvendes i kodeoptimering, huffman-kodning mv.
- Den maksimale højde af et B-træ er log M N (M er træens rækkefølge). I modsætning er binær træ maksimal højde log 2 N (N er antallet af noder og base er 2 fordi det er for binære).
Konklusion
B-træet bruges over binært og binært søgetræ. Hovedårsagen bag dette er hukommelseshierarkiet, hvor CPU'en er forbundet til cache med højbåndbreddekanalerne, mens CPU'en er forbundet til disk gennem lav båndbreddekanal. Et binært træ bruges, når optegnelser gemmes i RAM (lille og hurtig) og B-træ bruges, når arkiver gemmes i disk (stor og langsom). Så, brugen af B-træ i stedet for Binærtræ reducerer betydeligt adgangstiden på grund af høj forgreningsfaktor og reduceret højde af træet.