Sortering er en grundlæggende operation, hvor elementerne i et array er arrangeret i en bestemt rækkefølge for at forbedre dets søgbarhed. I enkle ord sorteres dataene, så det let kan søges.
Sammenligningstabel
| Grundlag for sammenligning | Indsætnings sortering | Valg Sorter |
|---|---|---|
| Grundlæggende | Dataene sorteres ved at indsætte dataene i en eksisterende sorteret fil. | Dataene sorteres ved at vælge og placere de på hinanden følgende elementer i sorteret placering. |
| Natur | stabil | Ustabil |
| Fremgangsmåde, der skal følges | Elementer er kendt på forhånd, mens placering for at placere dem søges. | Placering er tidligere kendt, mens elementer søges. |
| Umiddelbare data | Insertion sort er live sortering teknik, der kan beskæftige sig med øjeblikkelige data. | Det kan ikke beskæftige sig med øjeblikkelige data, det skal være til stede i starten. |
| Bedste tilfælde kompleksitet | På) | O (n2) |
Definition af Insertion Sort
Indsætnings sorter fungerer ved at indsætte værdisættet i den eksisterende sorteret fil. Det konstruerer den sorterede array ved at indsætte et enkelt element ad gangen. Denne proces fortsætter, indtil hele arrayet er sorteret i nogen rækkefølge. Det primære koncept bag indsættelsestype er at indsætte hvert emne på sit passende sted i den endelige liste. Indsætningssortemetoden gemmer en effektiv mængde hukommelse.
Arbejde med indsætnings sorteringen
- Det bruger to sæt arrays hvor man lagrer de sorterede data og andre på usorterede data.
- Sorteringsalgoritmen virker, indtil der er elementer i det usorterede sæt.
- Lad os antage, at der er 'n' talelementer i arrayet. Indledningsvis findes elementet med indeks 0 (LB = 0) i det sorterede sæt. Resterende elementer findes i den usorterede partition på listen.
- Det første element i den usorterede del har arrayindeks 1 (Hvis LB = 0).
- Efter hver iteration vælger den det første element i den usorterede partition og indsætter den på det rette sted i det sorterede sæt.
Fordele ved Insertion sort
- Nemt implementeret og meget effektiv, når den bruges sammen med små sæt data.
- Det ekstra lagerpladsbehov for indsættelsessortering er mindre (dvs. O (1)).
- Det anses for at være levende sorteringsmetode, da listen kan sorteres efterhånden som de nye elementer modtages.
- Det er hurtigere end andre sorteringsalgoritmer.
Eksempel:
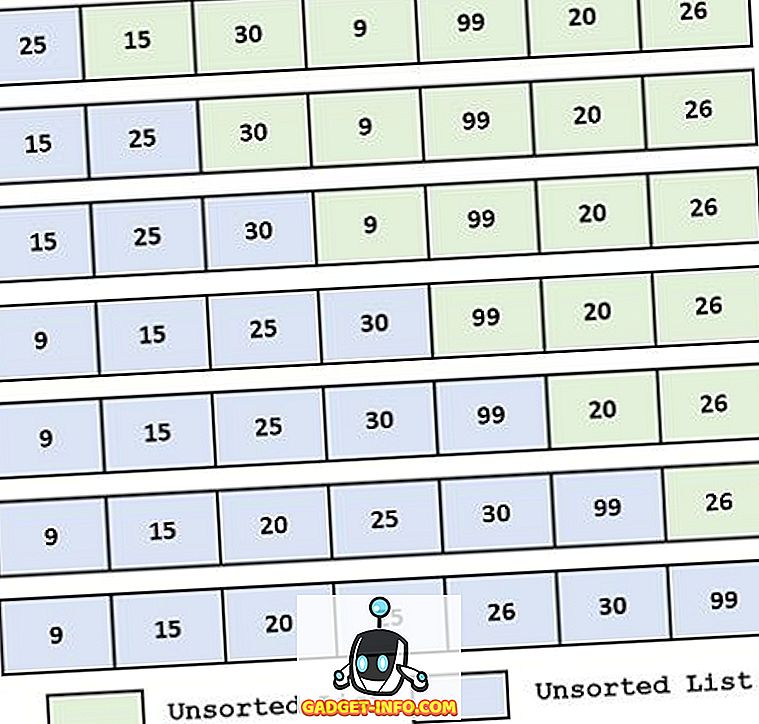
Definition af valg sortering
Valget Sortering udfører sortering ved at søge efter minimumsværdienummeret og placere det i første eller sidste position i henhold til ordren (stigende eller faldende). Processen med at søge minimale nøgle og placere den i den rigtige position fortsættes, indtil alle elementerne er placeret i rigtig position.
Arbejde med udvælgelsessorteringen
- Antag et array ARR med N elementer i hukommelsen.
- I den første passage søges den mindste nøgle sammen med sin position, så ARR [POS] byttes med ARR [0]. Derfor er ARR [0] sorteret.
- I den anden passage bestemmes positionen af den mindste værdi i underarrayet af N-1 elementer. Udveksle ARR [POS] med ARR [1].
- I passet N-1 udføres den samme proces for at sortere N-nummeret af elementer.
Eksempel:
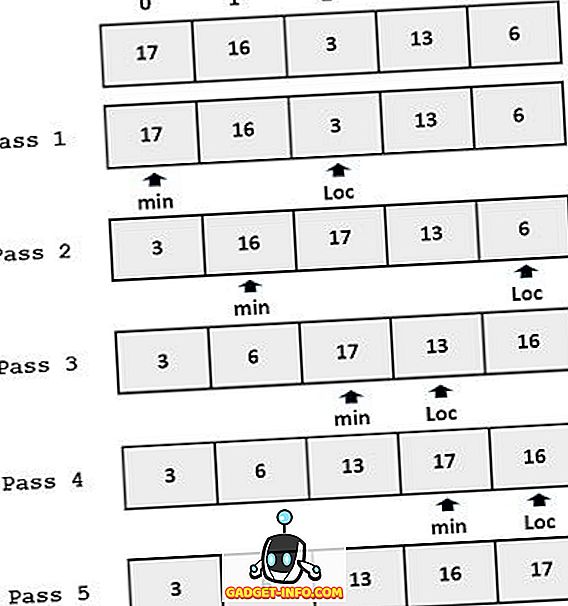
Nøgleforskelle mellem sortering af sortering og valg af sortering
- Indsætnings sorteringen udfører normalt indsætningen. Tværtimod udfører sorterings sorter udvælgelsen og placeringen af de krævede elementer.
- Indsætnings sorter siges at være stabile, mens valg sortering ikke er en stabil algoritme.
- I indføringssortalgoritmen er elementerne tidligere kendt. I modsætning hertil indeholder sorterings sorteringen placeringen på forhånd.
- Indsætningssort er en levende sorteringsteknik, hvor de ankomne elementer straks sorteres i listen, mens valg sortering ikke kan fungere godt med øjeblikkelige data.
- Indsætnings sorteringen har O (n) driftstid i bedste fald. Modsat er det bedste tilfælde at løbe tidskompleksiteten af udvalgssortet O (n2).
Kompleksiteten af indsættelsestype
Den bedst mulige kompleksitet af indsættelsestype er O (n) gange, dvs. når arrayet tidligere er sorteret. På samme måde, når arrayet er sorteret i omvendt rækkefølge, skal det første element i det usorterede array sammenlignes med hvert element i det sorterede sæt. Så i værste fald er kørselstiden for Insertion sort quadratisk, dvs. O (n2) . I gennemsnit skal det også lave mindste (k-1) / 2 sammenligninger. Derfor har den gennemsnitlige sag også kvadratisk driftstid O (n2).
Kompleksiteten af udvælgelsessorteringen
Som arbejdet med udvælgelse afhænger sorteringen ikke af den oprindelige rækkefølge af elementerne i arrayet, så der er ikke meget forskel mellem bedste tilfælde og værste tilfælde kompleksitet af valg sortering.
Valget sorterer vælger mindste værdi element, i udvælgelsesprocessen bliver alle 'n' antal elementer scannet; derfor foretages n-1 sammenligninger i første pass. Derefter byttes elementerne. På samme måde i det andet pass også for at finde det andet mindste element, kræver vi scanning af resten n-1 elementer, og processen fortsættes indtil hele sorteringen sorteres.
Således er kørestidskompleksiteten af udvalgssortet O (n2) .
= (n-1) + (n-2) + ......... .. + 2 + 1
= n (n-1) / 2 = 0 (n2)
Konklusion
Blandt begge sorteringsalgoritmen er indsættelsessorteringen hurtig, effektiv og stabil, mens valg sortering kun virker effektivt, når det lille sæt elementer er involveret eller listen er delvist sorteret tidligere. Antallet af sammenligninger foretaget ved valg sortering er større end de udførte bevægelser, mens i indsættelse sortere antallet af gange et element er flyttet eller byttet er større end sammenligningerne foretaget.