I modsætning til dette, i tilfælde af en kombination, betyder ordren slet ikke noget. Ikke kun i matematik, men også i det praktiske liv, gennemgår vi jævnligt disse to begreber. Selvom vi aldrig mærker det. Så læs artiklen omhyggeligt for at vide, hvordan disse to begreber er forskellige.
Sammenligningstabel
| Grundlag for sammenligning | permutation | kombination |
|---|---|---|
| Betyder | Permutation refererer til de forskellige måder at arrangere et sæt objekter i en sekventiel rækkefølge på. | Kombination refererer til flere måder at vælge emner fra et stort sæt objekter, så deres ordre ikke betyder noget. |
| Bestille | Relevant | Irrelevant |
| betegner | Arrangement | Udvælgelse |
| Hvad er det? | Bestilte elementer | Uordnede sæt |
| svar | Hvor mange forskellige arrangementer kan oprettes fra et givet sæt af objekter? | Hvor mange forskellige grupper kan vælges fra en større gruppe af objekter? |
| afledning | Multiputermutation fra en enkelt kombination. | Enkeltkombination fra en enkelt permutation. |
Definition af permutation
Vi definerer permutation som forskellige måder at arrangere nogle eller alle medlemmer af et sæt på i en bestemt rækkefølge. Det indebærer alle mulige arrangementer eller omlejringer af det givne sæt, i skelnelig rækkefølge.
For eksempel er alle mulige permutationer oprettet med bogstaver x, y, z -
- Ved at tage alle tre ad gangen er xyz, xzy, yxz, yzx, zxy, zyx.
- Ved at tage to ad gangen er xy, xz, yx, yz, zx, zy.
Samlet antal mulige permutationer af n ting taget r ad gangen kan beregnes som:
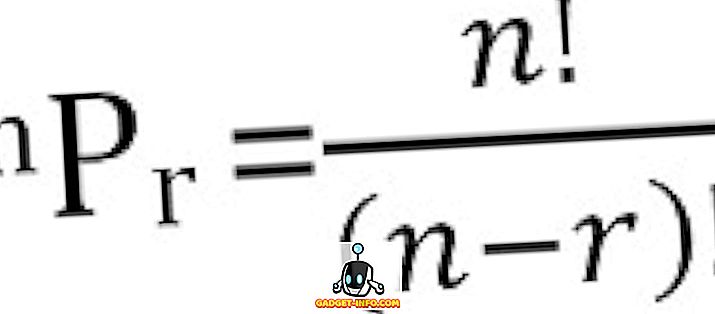
Definition af kombination
Kombinationen defineres som de forskellige måder at vælge en gruppe ved at tage nogle eller alle medlemmer af et sæt uden følgende rækkefølge.
For eksempel Alle mulige kombinationer valgt med bogstav m, n, o -
- Når tre ud af tre bogstaver skal vælges, er den eneste kombination mno
- Når to ud af tre bogstaver skal vælges, er de mulige kombinationer mn, nej, om.
Samlet antal mulige kombinationer af n ting taget r ad gangen kan beregnes som:
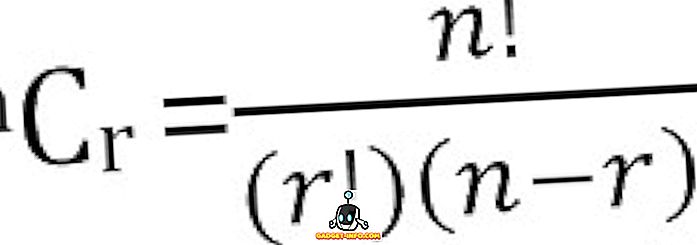
Nøgleforskelle mellem permutation og kombination
Forskellene mellem permutation og kombination er tegnet tydeligt af følgende grunde:
- Termen permutation henviser til flere måder at arrangere et sæt objekter i en sekventiel rækkefølge. Kombinationen indebærer flere måder at vælge emner fra en stor pulje af genstande, så deres ordre er irrelevant.
- Det primære kendetegn mellem disse to matematiske begreber er ordre, placering og position, dvs. i permutationsegenskaber nævnt ovenfor betyder noget, hvilket ikke betyder noget i tilfælde af kombinationen.
- Permutation angiver flere måder at arrangere tingene på, mennesker, cifre, alfabeter, farver osv. På den anden side angiver kombinationen forskellige måder at vælge menupunkter, mad, tøj, emner mv.
- Permutationen er intet andet end en ordnet kombination, mens kombination betyder uordnede sæt eller sammenkobling af værdier inden for specifikke kriterier.
- Mange permutationer kan stamme fra en enkelt kombination. Omvendt kan kun en enkelt kombination opnås fra en enkelt permutation.
- Permutation svar Hvor mange forskellige arrangementer kan oprettes fra et givet sæt af objekter? I modsætning til kombinationen, der forklarer, hvor mange forskellige grupper kan vælges fra en større gruppe af objekter?
Eksempel
Antag, at der er en situation, hvor du skal finde ud af det samlede antal mulige prøver af to ud af tre objekter A, B, C. I dette spørgsmål må du først forstå, om spørgsmålet er relateret til permutation eller kombination og den eneste måde at finde ud af dette er at kontrollere om ordren er vigtig eller ej.
Hvis ordren er signifikant, er spørgsmålet relateret til permutation, og mulige prøver vil være, AB, BA, BC, CB, AC, CA. Hvor AB er forskellig fra BA, er BC anderledes end CB og AC er anderledes CA.
Hvis ordren er irrelevant, så er spørgsmålet relateret til kombinationen, og de mulige prøver bliver AB, BC og CA.
Konklusion
Med ovenstående diskussion er det klart, at permutation og kombination er forskellige udtryk, som anvendes i matematik, statistik, forskning og vores daglige liv. Et punkt at huske, om disse to begreber er, at for et givet sæt objekter vil permutation altid være højere end dens kombination.
