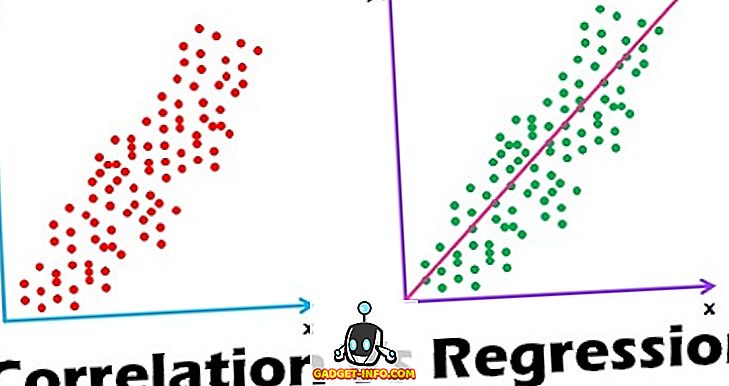
Forskellen mellem korrelation og regression er et af de ofte stillede spørgsmål i interviews. Desuden lider mange mennesker tvetydigt i at forstå disse to. Så læs denne artikel fuldt ud for at få en klar forståelse af disse to.
Sammenligningstabel
| Grundlag for sammenligning | Korrelation | Regression |
|---|---|---|
| Betyder | Korrelation er en statistisk foranstaltning, der bestemmer samforhold eller forening af to variabler. | Regression beskriver, hvordan en uafhængig variabel er numerisk relateret til den afhængige variabel. |
| Anvendelse | At repræsentere lineært forhold mellem to variabler. | At passe til en bedste linje og estimere en variabel på grundlag af en anden variabel. |
| Afhængige og uafhængige variabler | Ingen forskel | Begge variabler er forskellige. |
| indikerer | Korrelationskoefficienten angiver, i hvilket omfang to variabler bevæger sig sammen. | Regression angiver virkningen af en enhedsændring i den kendte variabel (x) på den estimerede variabel (y). |
| Objektiv | At finde en numerisk værdi, der udtrykker forholdet mellem variabler. | At estimere værdier af tilfældig variabel på grundlag af værdierne af den faste variabel. |
Definition af korrelation
Udtrykket korrelation er en kombination af to ord 'Co' (sammen) og relation (forbindelse) mellem to mængder. Korrelation er, når der på tidspunktet for undersøgelsen af to variabler observeres, at en enhedsændring i en variabel gengives ved en tilsvarende ændring i en anden variabel, dvs. direkte eller indirekte. Ellers siges variablerne ukorreleret, når bevægelsen i en variabel ikke udgør nogen bevægelse i en anden variabel i en bestemt retning. Det er en statistisk teknik, der repræsenterer styrken af forbindelsen mellem par af variabler.
Korrelation kan være positiv eller negativ. Når de to variabler bevæger sig i samme retning, dvs. en stigning i en variabel vil resultere i den tilsvarende stigning i en anden variabel og omvendt, så anses variablerne for at være positivt korrelerede. For eksempel : overskud og investering.
Tværtimod, når de to variabler bevæger sig i forskellige retninger, på en sådan måde, at en stigning i en variabel vil resultere i et fald i en anden variabel og omvendt, er denne situation kendt som negativ korrelation. For eksempel : Pris og efterspørgsel for et produkt.
Forholdsreglerne er angivet som under:
- Karl Pearsons produkt-moment korrelationskoefficient
- Spearmans rangkorrelationskoefficient
- Scatterdiagram
- Koefficient for samtidige afvigelser
Definition af regression
En statistisk teknik til estimering af ændringen i den metriske afhængige variabel som følge af ændringen i en eller flere uafhængige variabler baseret på det gennemsnitlige matematiske forhold mellem to eller flere variabler er kendt som regression. Det spiller en vigtig rolle i mange menneskelige aktiviteter, da det er et kraftfuldt og fleksibelt værktøj, som bruges til at forudsige tidligere, nuværende eller fremtidige begivenheder på baggrund af tidligere eller nuværende begivenheder. For eksempel : På baggrund af tidligere optegnelser kan en virksomheds fremtidige fortjeneste estimeres.
I en simpel lineær regression er der to variabler x og y, hvor y afhænger af x eller siger påvirket af x. Her kaldes y som afhængig, eller kriteriumvariabel og x er uafhængig eller forudsigelsesvariabel. Regressionslinjen for y på x er udtrykt som under:
y = a + bx
hvor, a = konstant,
b = regressionskoefficient,
I denne ligning er a og b de to regressionsparametre.
Nøgleforskelle mellem korrelation og regression
Punkterne nedenfor forklarer forskellen mellem korrelation og regression i detaljer:
- En statistisk foranstaltning, der bestemmer samforbindelsen eller foreningen af to mængder, kaldes korrelation. Regression beskriver, hvordan en uafhængig variabel er numerisk relateret til den afhængige variabel.
- Korrelation bruges til at repræsentere det lineære forhold mellem to variabler. Tværtimod anvendes regression til at passe den bedste linje og estimere en variabel på basis af en anden variabel.
- I korrelation er der ingen forskel mellem afhængige og uafhængige variabler, dvs. korrelation mellem x og y svarer til y og x. Omvendt er regressionen af y på x forskellig fra x på y.
- Korrelation angiver styrken af tilknytning mellem variabler. Til gengæld afspejler regression virkningen af enhedsændringen i den uafhængige variabel på den afhængige variabel.
- Korrelation sigter mod at finde en numerisk værdi, som udtrykker forholdet mellem variabler. I modsætning til regression, hvis mål er at forudsige værdier af den tilfældige variabel på grundlag af værdierne af den faste variabel.
Konklusion
Med ovenstående diskussion er det tydeligt, at der er stor forskel på disse to matematiske begreber, selv om disse to studeres sammen. Korrelation bruges, når forskeren ønsker at vide, om de undersøgte variabler er korrelerede eller ej, hvis ja, hvad er deres associations styrke. Pearsons korrelationskoefficient betragtes som den bedste måling af korrelation. I regressionsanalyse etableres et funktionelt forhold mellem to variabler for at fremstille fremtidige fremskrivninger på begivenheder.